Cường độ điện trường là gì? Công thức tính cường độ điện trường từ A-Z

Cường độ điện trường là gì?

Cường độ điện trường tại một điểm là đại lượng đặc trưng cho tác dụng lực của điện trường tại điểm đó. Ký hiệu là  E. Đơn vị của cường độ điện trường là Vôn/mét ký hiệu V/m

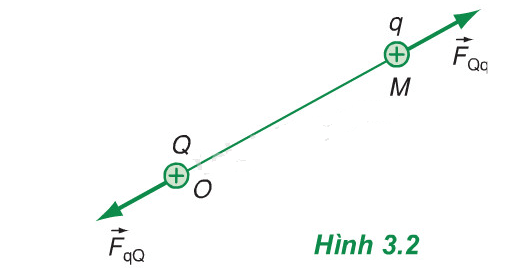
Giả sử có một điện tích điểm Q nằm tại điểm O. Điện tích này tạo ra một điện trường xung quanh nó. Để nghiên cứu điện trường của Q tại điểm M, ta đặt tại đó một điện tích điểm q, gọi là điện tích thử và xét lực điện tác dụng lên q (Hình 3.2). Theo định luật Cu-lông, q càng nằm xa Q thì lực điện càng nhỏ. Ta nói điện trường tại các điểm càng xa Q càng yếu. Vì thế cần phải xây dựng một khái niệm đặc trưng cho sự mạnh, yếu của điện trường tại một điểm.

Công thức tính cường độ điện trường

Cường độ điện trường được tính bằng thương của độ lớn lực điện F tác dụng lên 1 điện tích thử q (q lấy số dương) đặt tại điểm đó và độ lớn của q.

E = F/q

Trong đó:

• E là cường độ điện trường tại điểm mà ta xét
• F là độ lớn của lực tác dụng lên điện tích tại điểm đó
• q là độ lớn của điện tích

Công thức tính cường độ điện trường của một điện tích điểm

Cường độ điện trường của một điện tích điểm Q trong chân không

E = F/q = k.|Q|/r² = q/4πε₀εr²

Trong đó:

• E: Cường độ điện trường tại điểm cần xét
• q: Độ lớn của điện tích gây ra điện trường
• ε0: Hằng số điện môi chân không
• ε: Hằng số điện môi của môi trường cần xét
• r: Khoảng cách từ tâm điện trường tới điểm ta xét

Nguyên lý chồng chất điện trường: Một điểm M đặt trong điện trường do nhiều điện tích điểm gây ra thì cường độ điện trường tại M: E_M^→ = E₁^→ + E₂^→ + E₃^→ + …

Tham khảo thêm:

Bài tập ứng dụng công thức tính cường độ điện trường có lời giải

Dạng 1: Cách tính cường độ điện trường tại một điểm

Phương pháp:

E_M^→ có phương nằm trên đường thẳng nối điện tích điểm Q với điểm M

E_M^→ có chiều đi ra nếu Q dương, có chiều đi vào nếu Q âm

Độ lớn: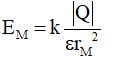 

Ví dụ 1: Tại hai điện tích điểm A và B cách nhau 5cm trong chân không có hai điện tích q₁ = +16.10^-8 C và q₂ = – 9.10^-8 C. Tính cường độ điện trường tổng hợp và vẽ vectơ cường độ điện trường tại điểm C nằm cách A một khoảng 4cm và cách B một khoảng 3cm.

Lời giải

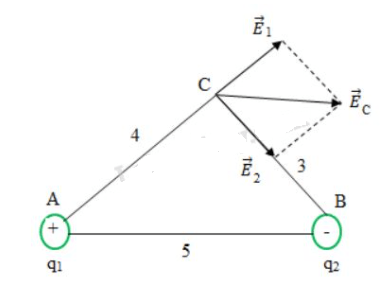
Gọi E₁^→, E₂^→ lần lượt là cường độ điện trường do q1 và q2 gây ra ở C.

Do AB = 5 cm; AC = 4 cm; BC = 3 cm => tam giác ABC vuông tại C.

Cường độ điện trường tổng hợp tại C:E_C^→ = E₁^→+ E₂^→

Ta có hình vẽ:

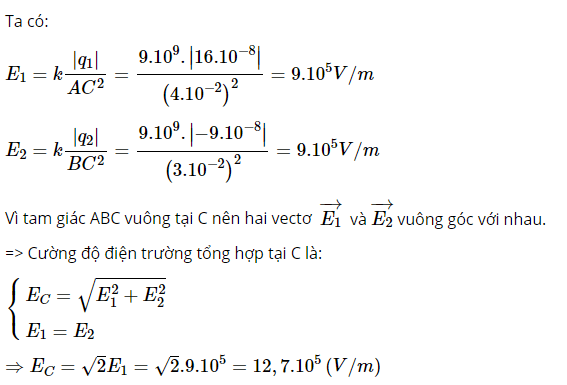
Ví dụ 2: Cho hai điểm A và B cùng nằm trên một đường sức điện do điện tích q > 0 gây ra. Biết độ lớn của cường độ điện trường tại A là 36 V/m, tại B là 9 V/m.

a. Xác định cường độ điện trường tại trung điểm M của AB.

b. Nếu đặt tại M một điện tích q₀ = -10^-2C thì lực điện tác dụng lên nó có độ lớn là bao nhiêu? Xác định phương chiều của lực này.

Lời giải

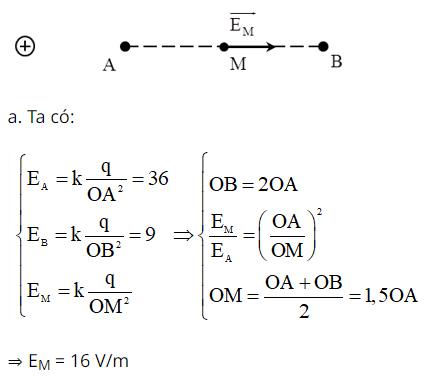
b. Lực điện do điện trường tác dụng lên điện tích q0 đặt tại M là:

F = |q₀|E = 0,16 N, ngược hướng với véctơ E.

Dạng 2: Cách xác định véctơ cường độ điện trường tổng hợp tại M

Phương pháp: Áp dụng nguyên lý chồng chất điện trường:

• Xác định phương, chiều, độ lớn của từng vectơ cường độ điện trường do từng điện tích gây ra.
• Vẽ vectơ cường độ điện trường tổng hợp (quy tắc hình bình hành).
• Xác định độ lớn của cường độ điện trường tổng hợp từ hình vẽ.

Khi xác định tổng của hai vectơ cần lưu ý các trường hợp đặc biệt: ↑↑, ↑↓,⊥, tam giác vuông, tam giác đều, … Nếu không xảy ra các trường hợp đặt biệt thì có thể tính độ dài của vectơ bằng định lý hàm cosin: a² = b² + c² – 2bc.cosA

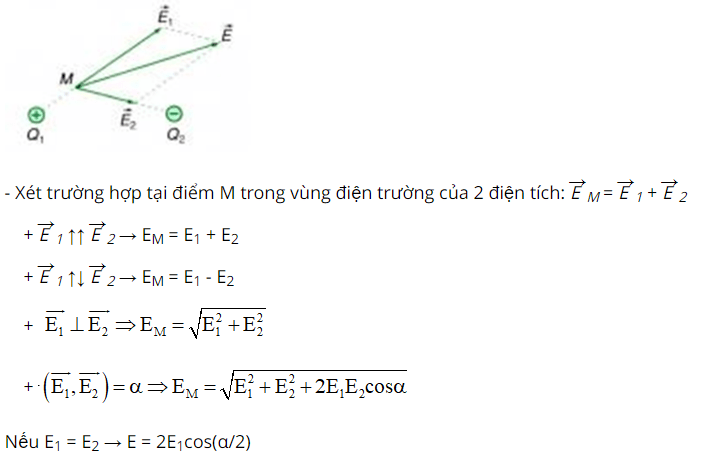
Ví dụ 1: Tại hai điểm A và B cách nhau 10 cm trong không khí có đặt hai điện tích q₁ = q₂ = 16.10^-8C. Xác định cường độ điện trường do hai điện tích điểm này gây ra tại

a. M với MA = MB = 5 cm.

b. N với NA = 5 cm, NB = 15 cm.

c. C biết AC = BC = 8 cm.

d. Xác định lực điện trường tác dụng lên q₃ = 2.10^-6 C đặt tại C.

Lời giải

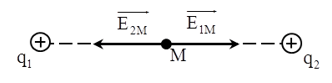
a. Ta có MA = MB = 5 cm và AB = 10 cm nên M là trung điểm của AB.

Vecto cường độ điện trường tại M là tổng hợp hai vecto cường độ điện trường do mỗi điện tích gây ra: E^→ = E^→_1M + E^→_2M

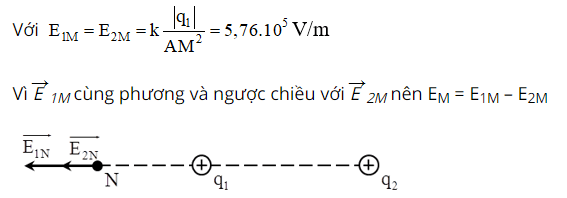
b. Ta có NA = 5 cm, NB = 15 cm và AB = 10 cm nên N nằm ngoài AB và nằm trên đường thẳng AB.

Vecto cường độ điện trường tại M là tổng hợp hai vecto cường độ điện trường do mỗi điện tích gây ra: E^→ = E^→_1N + E^→_2N

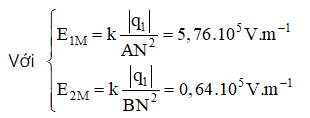
Vì E^→_1M cùng phương và cùng chiều với E^→_2M nên EM = E_1M + E_2M = 6,4.105 V/m

c. Ta có AC = BC = 8 cm và AB = 10 cm nên C nằm trên đường trung trực của AB.

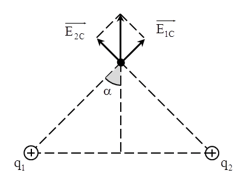
Tương tự, ta có vecto cường độ điện trường tổng hợp tại C sẽ là:

E_C = 2E_1Ccosα = 3,51.105 V/m

d. Lực điện trường tổng hợp tác dụng lên q₃ là F = q₃E = 0,7 N

Có chiều cùng chiều với E^→_C

Dạng 3: Cách xác định vị trí cường độ điện trường bằng 0

Phương pháp:

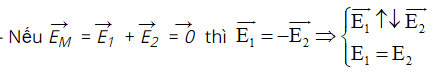
Trường hợp hai điện tích cùng dấu, q₁ > 0 đặt tại A và q₂ > 0 đặt tại B.

Gọi M là điểm có cường độ điện trường bị triệt tiêu:

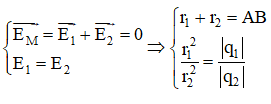
Trường hợp hai điện tích trái dấu, q₁ < 0 đặt tại A và q₂ > 0 đặt tại B.

Với |q₁| > |q₂| ⇒ M thuộc đường thẳng AB và ngoài đoạn AB, gần B hơn (r₁ > r₂)

Nếu E_M^→ = E₁^→ + E₂^→ + E₃^→ = 0^→ ⇒ E₃^→ = -(E₁^→ + E₂^→)….

Ví dụ: Cho hình vuông ABCD, tại A và C đặt các điện tích q₁ = q₃ = q. Hỏi phải đặt tại B một điện tích bao nhiêu để cường độ điện trường tại D bằng 0.

Lời giải

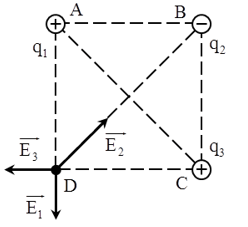
Cường độ điện trường tổng hợp tại đỉnh D của hình vuông:

ED^→ = E₁^→ + E₂^→ + E₃^→, trong đó E₁^→, E₂^→, E₃^→ lần lượt là cường độ điện trường do q₁, q₂, q3 gây ra tại D.

+ Để cường độ điện trường tại D bị triệt tiêu thì ED^→ = 0

Vì q₁ = q₃ và AD = CD nên E₁ = E₃ và cường độ điện trường tổng hợp

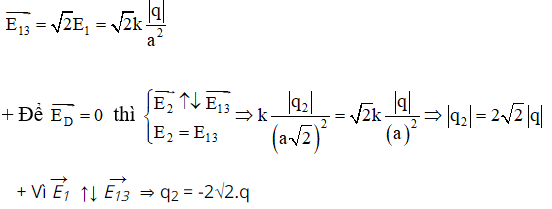
Bên trên chính là toàn bộ lý thuyết và công thức tính cường độ điện trường có thể giúp các bạn áp dụng vào làm bài tập nhé