Nội Dung Bài Viết
7 hằng đẳng thức đáng nhớ là những đẳng thức cơ bản được chứng minh bằng phép nhân đa thức với đa thức, được sử dụng thường xuyên để giải phương trình, nhân chia các đa thức… Trong bài viết dưới đây, smarthack.vn sẽ giúp bạn tổng hợp 7 hằng đẳng thức đáng nhớ chính xác, đầy đủ từ cơ bản tới mở rộng nâng cao, cùng tìm hiểu nhé!.
Tìm hiểu 7 hằng đẳng thức đáng nhớ cơ bản
Trong toán học, hằng đẳng thức đáng nhớ là những đẳng thức cơ bản được chứng minh bằng phép nhân đa thức với đa thức. Những đẳng thức này được sử dụng thường xuyên trong các bài toán liên quan đến giải phương trình, nhân chia các đa thức, biến đổi biểu thức tại cấp học trung học cơ sở và trung học phổ thông.
Bạn đang xem: Hằng đẳng thức (a+b+c)^3
Tóm tắt 7 hằng đẳng thức đáng nhớ
Trong những hằng đẳng thức này, ta có một bên dấu bằng sẽ là tổng hoặc hiệu và bên gọi lại là tích hoặc lũy thừa. Dưới đây là bảng hằng đẳng thức đáng nhớ dành cho bạn:
| Bình phương của một tổng | ((a+b)^{2}= a^{2}+2ab+b^{2}) |
| Bình phương của một hiệu | ((a-b)^{2}= a^{2}-2ab+b^{2}) |
| Hiệu hai bình phương | (a^{2}-b^{2}=(a+b)(a-b)) |
| Lập phương của một tổng | ((a+b)^{3}= a^{3}+3a^{2}b +3ab^{2}+b^{3}) |
| Lập phương của một hiệu | ((a-b)^{3}= a^{3}-3a^{2}b +3ab^{2}-b^{3}) |
| Tổng hai lập phương | (a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})) |
| Hiệu hai lập phương | (a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})) |
Phát biểu 7 hằng đẳng thức đáng nhớ bằng lời
1. Bình phương của 1 tổng sẽ bằng bình phương của số thứ 1 cộng với hai lần tích của số thứ nhất với số thứ hai cộng bình phương số thứ hai
2. Bình phương của 1 hiệu sẽ bằng bình phương của số thứ 1 trừ 2 lần tích số thứ nhất với số thứ 2 cộng với bình phương số thứ 2.
3. Hiệu của 2 bình phương sẽ bằng tích của tổng 2 số với hiệu 2 số.
4. Lập phương của 1 tổng sẽ bằng với lập phương số thứ 1 + 3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 + lập phương số thứ 2.
Xem thêm: So Sánh Giá Trị Thặng Dư Tương Đối Và Giá Trị Thặng Dư Siêu Ngạch
5. Lập phương của 1 tổng sẽ bằng với lập phương số thứ 1 -3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 – lập phương số thứ 2.
6. Tổng hai lập phương sẽ bằng tích giữa tổng 2 số với bình phương thiếu của 1 hiệu.
7. Hiệu của 2 lập phương sẽ bằng với tích giữa hiệu hai số với bình phương thiếu của 1 tổng.
Các hằng đẳng thức mở rộng thường gặp
Hằng đẳng thức đáng nhớ với hàm bậc 2
((a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc)((a+b-c)^{2}=a^{2}+b^{2}+c^{2}+2ab-2ac-2bc)((a-b-c)^{2}=a^{2}+b^{2}+c^{2}-2ab-2ac+2bc)
Hằng đẳng thức đáng nhớ với hàm bậc 3
(a^3 + b^3 = (a+b)^3 – 3ab(a + b))(a^3 – b^3 = (a – b)^3 + 3ab(a – b))((a+b+c)^{3}=a^{3}+b^{3}+c^{3}+3(a+b)(a+c)(b+c))(a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca))((a – b)^3 + (b – c)^3 + (c – a)^3 = 3(a – b)(b – c)(c – a))((a + b)(b + c)(c + a) – 8abc = a(b – c)^2 + b(c – a)^2 + c(a – b)^2)((a + b)(b+c)(c+a) = (a+b+c)(ab+bc+ca)-abc)((a + b)(b + c)(c + a) – 8abc = a(b – c)^2 + b(c – a)^2 + c(a – b)^2)((a + b)(b+c)(c+a) = (a+b+c)(ab+bc+ca)-abc)
Hằng đẳng thức dạng tổng quát
(a^{n}+b^{n}=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^{2}-a^{n-4}b^{3}+…+a^{2}b^{n-3}-a.b^{n-2}+b^{n-1})) (1) với n là số lẻ thuộc tập N
(a^n – b^n = (a – b)(a^{n – 1} + a^{n – 2}b + a^{n – 3}b^2 + … + a^2b^{n – 3} + ab^{n – 2} + b^{n – 1} ))
Tìm hiểu nhị thức Newton là gì?
((a + b)^{n} = sum_{k = 0}^{n}C^{k}_{n}a^{n – k}b^{k})
Với (a, b epsilon mathbb{R}, n epsilon mathbb{N}^{*})
Bài tập về 7 hằng đẳng thức đáng nhớ





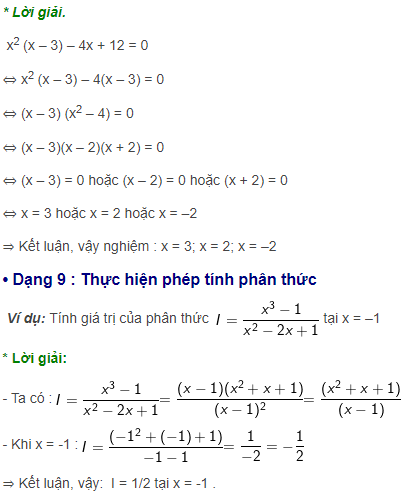
Vận dụng hằng đẳng thức đáng nhớ
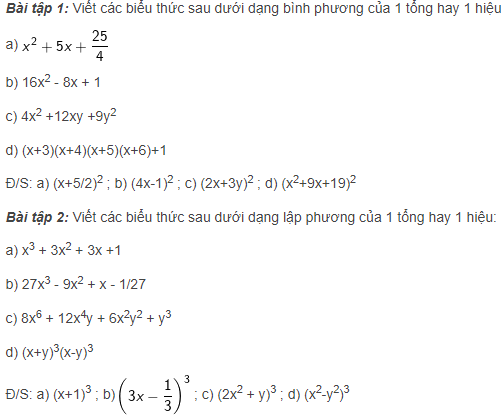


Trên đây là bài viết tổng hợp kiến thức về các hằng đẳng thức đáng nhớ cơ bản và mở rộng. Nếu có đóng góp hay thắc mắc gì về chủ đề 7 hằng đẳng thức đáng nhớ, các bạn đừng quên bình luận bên dưới nhé! Chúc bạn luôn học tốt!.
Chuyên mục:
Chuyên mục: Nhà Cái Uy Tín
Source: Minh Gà Chọi










